При записи математических выражений могут использоваться четыре стандартные арифметрические операции (+, -, *, /) и операция возведения в степень (^, ^^ или **). Приоритет этих операций традиционен, для изменения порядка вычислений следует использовать круглые скобки. Кроме чисел выражения могут содержать результаты вычислений математических функций. Аргументы функций указываются в круглых скобках, например, запись sqrt(5) означает корень квадратный из числа 5. Если в результате расчета получается дробное выражение, то оно и выводится в виде обыкновенной дроби. Иррациональные числа, входящие в выражение, представляются в символьном виде.
Для раскрытия скобок используется функция expand. Команда ev позволит получить численное значение выражения. Ее первый аргумент есть вычисляемое выражение, а второй - опция numer. Напомним, что символ % означает результат предыдущего вычисления.
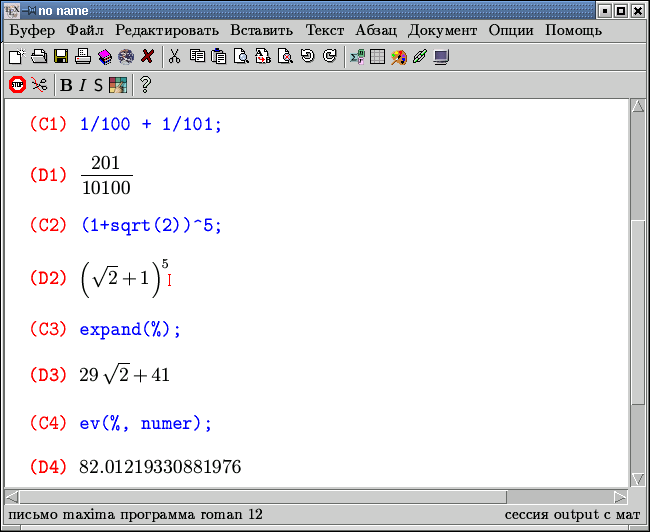
На рисунке изображен пример работы с оболочкой texmacs. Дальнейший вывод соответствует работе с программой maxima (xmaxima).
Допускается более удобная форма функции ev, требующая указания только ее аргументов:
(C5) 29*sqrt(2) + 41, numer; (D5) 82.01219330881976
По умолчанию результат содержит 16 значащих цифр. Для вывода числа в экспоненциальной форме используется функция bfloat:
(C6) bfloat(d3); (D6) 8.201219330881976B1
Запись mBn есть сокращенная форма выражения m*10n.
Количество значащих цифр в представлении числа определяется специальной переменной FPPREC. Увеличение ее значения приводит к возрастанию точности результата, например,
(C7) fpprec; (D7) 16 (C8) fpprec:100; (D8) 100 (C9) ''c5; (D9) 8.20121933088197607657604923686248525# 030775305167218616484631047782707024434954# 8350683851114422615155B1
Символ # в конце выводимой строки означает, что число не уместилось на одной строке и его оставшаяся часть переносится на следующую. В последнем примере мы использовали повторение ранее введенной команды (''c5).
Система Maxima может работать с числами произвольной длины и точности:
(C10) 100!; (D10) 933262154439441526816992388562667004# 9071596826438162146859296389521759999322991# 5608941463976156518286253697920827223758251# 185210916864000000000000000000000000
Пример
Вычислим число PI с точностью 200 знаков после запятой:
(C11) %PI, numer; (D11) 3.141592653589793 (C12) fpprec:200; (D12) 200 (C13) bfloat(%PI); (D13) 3.141592653589793238462643383279502884# 19716939937510582097494459230781640628620899# 86280348253421170679821480865132823066470938# 44609550582231725359408128481117450284102701# 9385211055596446229489549303819B0
Если требуется вывод с увеличенной точностью только для результатов нескольких команд, то следует использовать функцию block. Первым аргументом этой функции является список локальных переменных, т. е. переменных, значения которых будут восстановлены после завершения выполнения команд блока. При указании таких переменных возможно присваивание им временных значений. После списка локальных переменных через запятую указывается последовательность команд.
(C14) FPPREC:16; (D14) 16 (C15) bfloat(%PI); (D15) 3.141592653589793B0 (C16) block([FPPREC:100], bfloat(%PI)); (D16) 3.14159265358979323846264338327950# 2884197169399375105820974944592307816406# 286208998628034825342117068B0 (C17) ''c15; (D17) 3.141592653589793B0
В Maxima доступны прямые и обратные тригонометрические функции: sin (синус), cos (косинус), tan (тангенс), cot (котангенс), asin (арксинус), acos (арккосинус), atan (арктангенс), acot (арккотангенс). Кроме них имеются две менее известные функции - секонс (sec x = 1/cos x) и косеконс (csc x = 1/sin x).
(C18) block([FPPREC:100],sin(bfloat(%PI))); (D18) - 2.570579198029723711689569064713781# 2738478411385601247337570449378000209830368# 31739403591933813645377B-101 (C19) block([FPPREC:100],sin(%PI)) ; (D19) 0 (C20) sin(%PI/6)^2 +cos(%PI/6)^2; (D20) 1 (C21) sec(%PI/3); (D21) 2 (C22) asin(1/2); %PI (D22) --- 6
К сожалению, Maxima не может в символьном виде вычислить значения обратных тригонометрических функций в некоторых точках:
(C23) asin(sqrt(3)/2); SQRT(3) (D23) ASIN(-------) 2 (C24) %, expand; SQRT(3) (D24) ASIN(-------) 2
Для вычисления натурального логарифма используется функция log:
(C25) log(%E^2); (D25) 2 (C26) 5*log(a)+6*log(b); (D26) 6 LOG(b) + 5 LOG(a) (C27) logcontract(%); 5 6 (D27) LOG(a b )