Работа с выражениями

Для запуска программы наберите команду mathematica в командном окне, либо в стартовом меню выберите пункт Mathematica.

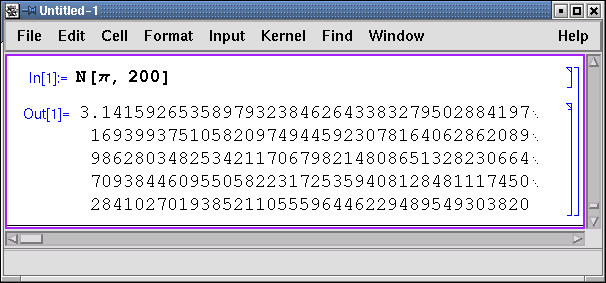
При старте открывается рабочее окно, в котором отображаются ввод и вывод программы. В верхней его части находится меню, позволяющее выполнять различные действия, в том числе сохранение текущей сессии в файле с расширением nb. Кроме основного окна в работе участвуют так называемые палитры. Если они не появились при старте, то для их открытия можно воспользоваться пунктом Palettes из меню File. Палитра Basic Input предоставляет набор кнопок для ввода наиболее употребительных символов, таких как корни, дроби, интегралы, буквы греческого алфавита и т. д. Палитра Basic Calculations содержит шаблоны для вычисления основных алгебраических функций.

Чтобы инициировать процесс вычисления после набора команды нужно одновременно нажать клавиши Shift и Enter (либо клавишу Enter на числовой клавиатуре справа). После завершения расчета программа присваивает имена вида In[1] и Out[1] исходному выражению и результату. Можно отменить показ имен, отключив в меню Kernel пункт Show In/Out Names.

Mathematica в качестве имен функций почти всегда использует их английские названия. Исключениями являются несколько наиболее употребимых функций: кроме N для определения численного значения, символ D используется для нахождения производной.

Дополнительную информацию о назначении той или иной функции в ходе работы с системой можно получить, используя следующие команды:

? Name	- помощь по заданному слову Name;
?? Name	- расширенная помощь по заданному слову Name.

Большинство функций программы Mathematica являются встроенными, т. е. становятся доступными сразу после загрузки системы. Кроме того, имеется набор так называемых пакетов расширения, содержащих специализированные функции для работы в той или иной области. Среди них Algebra, Calculus, DiscreteMath, Geometry, LinearAlgebra, Miscellaneous, Graphics, NumberTheory, NumericalMath, Statistics и некоторые другие. Каждый из пакетов содержит набор подпакетов, например, в пакет Algebra входят такие подпакеты, как InequalitySolve для решения неравенств, SymbolicSum для вычисления сумм рядов, Trigonometry для работы с тригонометрическими выражениями и другие. Для того чтобы сделать доступными функции, входящие в состав специализированных пакетов, следует их подключить командой типа

Needs["Algebra`Trigonometry`"]

или

< (обратите внимание на использование обратных апострофов). Если загружаемый подпакет содержит несколько функций, то их перечень выводится на экран. При наличии в пакете только одной функции ее имя совпадает с именем пакета.

Mathematica всегда старается упростить введенное выражение. Если вы попробуете вычислить корень квадратный из двадцати, для чего после ввода соответствующего выражения нажмете Shift+Enter, то результатом окажется выражение, равное двум корням из пяти. Программа упростит выражение, оставив его в символьном виде. Для того чтобы получить численное значение выражения expr, следует использовать функцию N[expr] или N[expr, n], где n задает точность вычислений. По умолчанию выводится значение выражения с пятью знаками после запятой.

	Для ввода выражений удобно пользоваться палитрой Basic Input, которая содержит шаблоны для ввода степеней, дробей, радикалов, греческих букв и т. п. При выборе соответствующего шаблона появляется возможность ввести нужные значения (место для ввода значений выглядит как небольшой квадратик). Отметим некоторые особенности синтаксиса системы, используемого при записи арифметических выражений:   знак умножения может быть заменен пробелом;   имена встроенных функций начинаются с большой буквы;   параметры функций задаются в квадратных скобках, например Sin[2];   круглые скобки используются для того, чтобы выделить части выражений и изменить порядок выполнения операций;   фигурные скобки используются при задании списков, например, при перечислении уравнений, входящих в систему.

Mathematica допускает использование чисел четырех видов: целые, рациональные, вещественные и комплексные. Все типы чисел могут содержать любое количество цифр. Чтобы число рассматривалось как вещественное, оно должно содержать точку в его записи, даже если дробная часть равна нулю, например, 2. или 2.0.

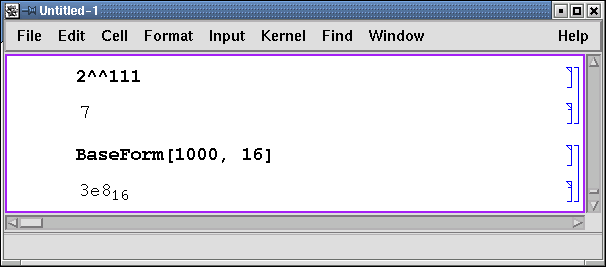
Для перевода числа, заданного в системе счисления с произвольным основанием, в десятичную используется конструкция Основание^^Число, а для обратного перевода числа a из десятичной системы в систему с основанием n (где n не превышает 32) - функция BaseForm[a, n].

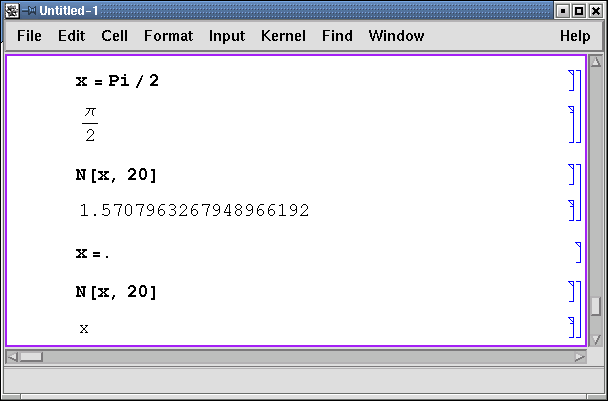
Инициализация переменных осуществляется при помощи операции =, для аннулирования значения переменной следует после знака равно указать символ . (точка).

При выполнении вычислений особая роль отводится символу % - он означает результат предыдущей операции. Комбинация символов %% соответствует результату операции, выполненной перед предыдущей, и так далее.

Для того чтобы "заставить" систему упростить выражение, используется функция Simplify. Ниже приведены примеры использования этой функции.

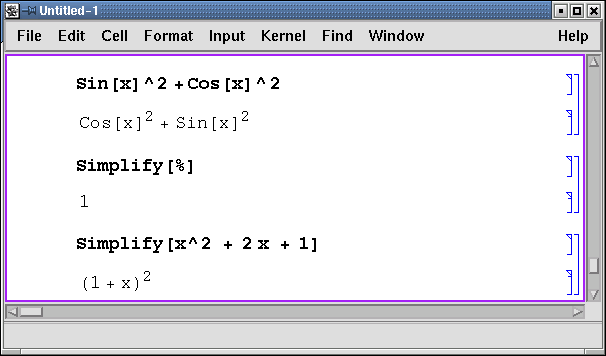
Функция Expand раскрывает скобки в выражении. Например, в результате выполнения команды Expand[(a + b)³] получится a³ + 3a²b + 3ab² + b³.

К сожалению, функция Simplify не всегда выдает самый простой результат. В этом случае можно использовать функцию FullSimplify.

 

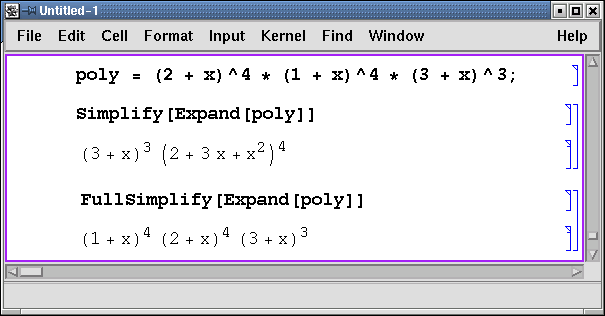
В этом примере мы сначала завели переменную poly для хранения многочлена, что позволило в дальнейшем избежать его повторного ввода. Упрощение результата раскрытия скобок не приводит к исходному выражению, которое получается только после применения функции FullSimplify.

Обратите внимание на символ ; (точка с запятой) в конце ввода многочлена. Этот символ препятствует выводу на экран результата обработки программой Mathematica введенного выражения.

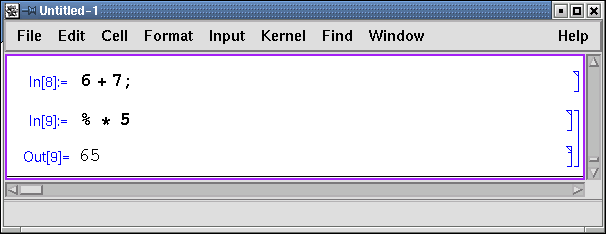
Разложение на множители, если это возможно, осуществляет функция Factor. Эта функция может работать и с тригонометрическими выражениями, но в этом случае нужно использовать дополнительную опцию Trig -> True:

In[10]:= Factor[x^4+8x^3+17x^2+16x+30]
Out[10]= (3 + x)(5 + x)(2 + x^2)

In[11]:= Factor[Sin[6x]/Sin[2x] + Cos[6x - Pi]/Cos[2x], 
 Trig -> True]
Out[11]= 2

Напомним, это многочленом P(x)степени n от переменной x называется выражение вида

a₀xⁿ+a₁x^n-1+...+ a_n-1x+a_n.

Для вынесения общего числового множителя в многочлене за скобки предназначена функция FactorTerms[poly, x], где poly есть многочлен от переменной x. Для получения списка коэффициентов при степенях x, начиная с нулевой, используется функция CoefficientList[poly, x].

In[12]:= FactorTerms[1232x^4+168x+144, x]
Out[12]= (8 ((18 + 21x + 154x^4))

In[13]:= CoefficientList[12x^4+68x+44,x]
Out[13]= {44,68,0,0,12}

Некоторые другие функции для работы с многочленами приведены в следующей таблице.

PolynomialGCD[poly1, poly2]	Нахождение наибольшего общего делителя poly1 и poly2
PolynomialLCM[poly1, poly2]	Нахождение наименьшего общего кратного
PolynomialQuotient[poly1, poly2, x]	Нахождение частного от деления poly1 на poly2
PolynomialRemainder[poly1, poly2, x]	Нахождение остатка от деления poly1 на poly2

 

Пример
Пусть P₁(x)= x⁴+2x³-4x²-5x-6. Определим, является ли число 2 корнем уравнения P₁(x)=0. Известно, что многочлен делится без остатка на выражение x-x₀, где x₀ - корень уравнения. Найдем остаток от деления P₁(x) на x-2:

PolynomialRemainder[x^4+2x^3-4x^2-5x-6, x-2 , x].

Результат равен 0, следовательно 2 - корень данного уравнения.

Задания

1. Вычислитe 2^-10 с точностью 20 знаков после запятой.
2. Упростите выражение .
3. Разложите на множители выражение
   x⁶-18x⁵+135x⁴-540x³+ 1215x²-1458x+729.
4. Найдите остаток от деления многочлена P₁(x) на x-1.
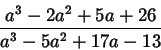