Матрицы

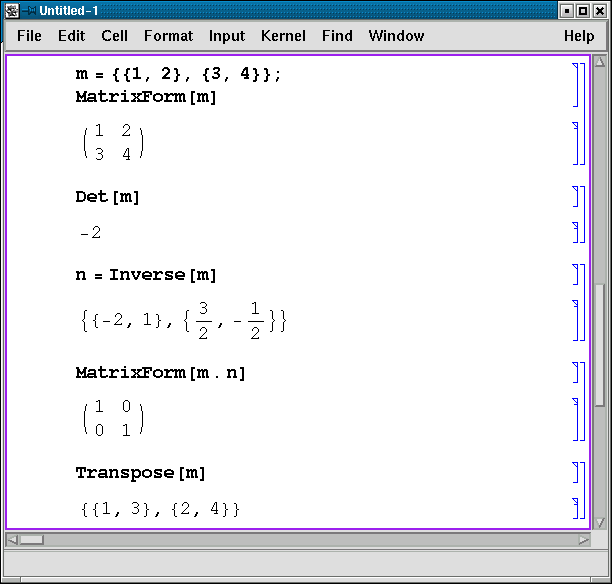
Матрица задается как список списков элементов строк. Для представления списка в традиционной матричной форме используется функция MatrixForm. Процедура Det позволяет вычислять определитель. С помощью функции Dot находится произведение матриц и векторов, но можно использовать и символ . (точка). Inverse находит обратную матрицу, а Transpose используется для транспонирования матрицы (превращения каждой строки в столбец с тем же номером).

Для решения систем линейных уравнений можно использовать функцию LinearSolve или матричный метод, при котором матрица X, содержащая значения неизвестных, находится по формуле X = A^-1 . B, где . означает операцию умножения матриц.

Пример
Используем указанные способы при решении следующей системы уравнений:

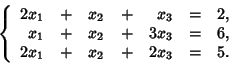
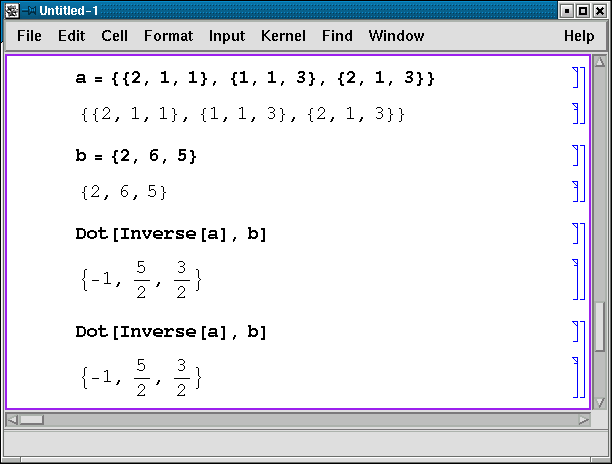
Итак, решением данной системы является тройка {-1, 2.5, 1.5}.

Задания

1. Найдите произведение матриц A и B, где
   ,   .
2. Транспонируйте матрицу B и найдите ее определитель.
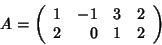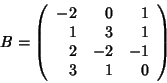